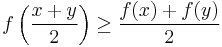Concave function
In mathematics, a concave function is the negative of a convex function. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap or upper convex.
Contents |
Definition
A real-valued function f on an interval (or, more generally, a convex set in vector space) is said to be concave if, for any x and y in the interval and for any t in [0,1],
A function is called strictly concave if
for any t in (0,1) and x ≠ y.
For a function f:R→R, this definition merely states that for every z between x and y, the point (z, f(z) ) on the graph of f is above the straight line joining the points (x, f(x) ) and (y, f(y) ).
A function f(x) is quasiconcave if the upper contour sets of the function 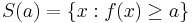 are convex sets.[1]
are convex sets.[1]
Properties
A function f(x) is concave over a convex set if and only if the function −f(x) is a convex function over the set.
A differentiable function f is concave on an interval if its derivative function f ′ is monotonically decreasing on that interval: a concave function has a decreasing slope. ("Decreasing" here means "non-increasing", rather than "strictly decreasing", and thus allows zero slopes.)
For a twice-differentiable function f, if the second derivative, f ′′(x), is positive (or, if the acceleration is positive), then the graph is convex; if f ′′(x) is negative, then the graph is concave. Points where concavity changes are inflection points.
If a convex (i.e., concave upward) function has a "bottom", any point at the bottom is a minimal extremum. If a concave (i.e., concave downward) function has an "apex", any point at the apex is a maximal extremum.
If f(x) is twice-differentiable, then f(x) is concave if and only if f ′′(x) is non-positive. If its second derivative is negative then it is strictly concave, but the opposite is not true, as shown by f(x) = -x4.
If f is concave and differentiable then
A continuous function on C is concave if and only if for any x and y in C
If a function f is concave, and f(0) ≥ 0, then f is subadditive. Proof:
- since f is concave, let y = 0,
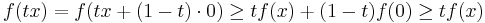
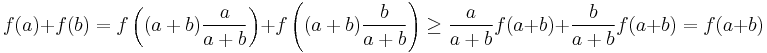
Examples
- The functions
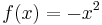 and
and 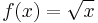 are concave, as the second derivative is always negative.
are concave, as the second derivative is always negative. - Any linear function
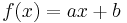 is both concave and convex.
is both concave and convex. - The function
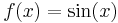 is concave on the interval
is concave on the interval ![[0, \pi]](/2012-wikipedia_en_all_nopic_01_2012/I/e1868564b62b4e2f1c063321df289469.png) .
. - The function
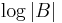 , where
, where 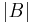 is the determinant of a nonnegative-definite matrix B, is concave.[3]
is the determinant of a nonnegative-definite matrix B, is concave.[3] - Practical example: rays bending in Computation of radiowave attenuation in the atmosphere.
See also
- Concave polygon
- Convex function
- Jensen's inequality
- Logarithmically concave function
- Quasiconcave function
References
- ^ Varian, Hal A. (1992) Microeconomic Analysis. Third Edition. W.W. Norton and Company. p. 496
- ^ Varian, Hal A. (1992) Microeconomic Analysis. Third Edition. W.W. Norton and Company. p. 489
- ^ Thomas M. Cover and J. A. Thomas (1988). "Determinant inequalities via information theory". SIAM journal on matrix analysis and applications 9 (3): 384–392.
- Crouzeix, J.-P. (2008). "Quasi-concavity". In Durlauf, Steven N.; Blume, Lawrence E. The New Palgrave Dictionary of Economics (Second ed.). Palgrave Macmillan. doi:10.1057/9780230226203.1375. http://www.dictionaryofeconomics.com/article?id=pde2008_Q000008.
- Rao, Singiresu S. (2009). Engineering Optimization: Theory and Practice. John Wiley and Sons. p. 779. ISBN 0470183527.
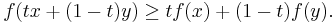
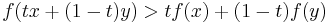
![f(y) \leq f(x) %2B f'(x)[y-x]](/2012-wikipedia_en_all_nopic_01_2012/I/268ec95745a1494883bcb3d5af2ff2f3.png)